大嘎好!时隔两月我又回来了!
5 r0 l/ U2 C8 N. M/ I' A好久没写文章了,刚好最近做隐马尔可夫的二次探索有了新的发现和理解,和大家分享一下。本文含有大量分析源码,感兴趣的朋友也可以自己用其它模型尝试分析~# W! f$ ^3 h* x' f3 J0 ?* k* I
& ^) ?2 `& Y9 n5 s/ A/ B) _
3 o% a+ A9 w& t8 S5 j大家都知道西蒙斯就是靠HMM做择时一炮打红的,隐马尔可夫模型作为一个经典的概率模型可解释性很强,可探索性也很强,它不需要复杂的特征工程,直接从价格波动本身出发就可以做分析。
7 t, g* o# C9 U* N有关隐马尔可夫模型的原理本文不详述,简单来说就是你能看到的每一个状态(显性状态)其实背后都有一个对应的隐性状态,而隐形状态之间是依据马尔可夫过程进行状态转移的,比如显性状态是今天你喜欢的姑娘没出门,隐性状态是因为今天下雨了,那么你通过天气预告知道明天不下雨的概率(隐性状态转移概率),那你就可以大概估摸着到底哪天去约你喜欢的姑娘出去吃饭了。
! w+ q) O3 D2 d( THMM的假设是比较理想的,也就是隐性状态是可枚举而且独立的,在金融序列中,人们已经人为地确定过一些价格状态,比如拉盘/砸盘/横盘等,那么在这个基础上,我们是否可以假定知道价格的所有状态,然后对应的去寻找隐性状态的转移概率呢?/ `' S# _' W# ^# p5 d# z: k; Y* j" T/ g
<hr/>1. 准备工作6 s8 b' T9 G& f$ M0 K5 [; E
那么首先导入需要的库和数据提取,我使用的数据集为ETH/USDT永续合约5min级bar级数据,数据的时间范围为2020-09-26 08:00:00 到 2021-08-11 20:25:00,共计数据条数为92022条。- d/ R) a0 G' ]; s1 w) p; A
此外,本文中使用的隐马尔可夫模型开源库为hmmlearn。
- n% b( c2 x6 x" y% o- ~import numpy as np
9 g7 X5 p7 \' W" qimport pandas as pd) [3 J( u9 h }" L5 \
import matplotlib.pyplot as plt
. {) V+ H- S, G9 s/ ~& Mimport warnings9 O: e; N0 D7 R4 \; H/ I
warnings.filterwarnings('ignore')
5 E; P; D6 _, u9 n& {from tqdm import tqdm Y) F6 O; B1 o+ e! \
import random
9 K- K/ d6 O1 T+ f: S- n N5 N$ Fimport datetime
% u q! a/ P$ w6 {4 v& kfrom hmmlearn.hmm import GaussianHMM,GMMHMM,MultinomialHMM1 c# }; s5 R# R0 i
from sklearn.model_selection import train_test_split
. Z1 a/ F2 n4 m! qimport itertools! v# o% C0 ~. ]' z* H1 }- y
1 r' C9 i- [, J( M. |% z# pdf = pd.read_csv('5m.csv')2. 特征提取 . H7 ?, q! \$ N* r) I& I
虽然不需要做复杂的特征工程,但是简单的特征工程还是要做滴!毕竟要做价格状态的判断,单纯依据价格本身是很不合理的,而bar级数据中包含了OHLC四维特征,从价格本身和波动率来判断的话,可以做以下三种不同特征:1 c! p: i9 L7 w+ O
bar级价格变化率: (close-open)/open
" }, y! Y2 G- M- Z! f/ a7 wbar级上涨随机波动: (high-open)/open/ T+ T" P& l- q! {# [/ O* O+ Q
bar级下跌随机波动: (low-open)/open
$ s F$ g6 v+ B1 x( G那么就可以定义一个提取特征的函数了:
& R3 J5 S s5 ~' \, @def _extract_features(data):% G/ n6 v7 N* n; i
open_price = np.array(data['开盘价'])
6 _5 [9 t& f. _ ]' [ close_price = np.array(data['收盘价'])
( G2 E' K4 C- {4 i high_price = np.array(data['最高价'])
6 F3 O" k u) E7 D/ t; n low_price = np.array(data['最低价'])% i1 X1 S8 Q$ D: F( F* ?
& \! Y2 C2 k1 ~2 W; ^0 z! _. x6 Z # 计算收盘价、高价和低价的分数变化
+ T) t' g; f* v- @6 m- ?6 m frac_change = (close_price - open_price) / open_price
9 _' E3 o) R7 }2 q: n! B frac_high = (high_price - open_price) / open_price" F' I* Y# {5 l% F
frac_low = (low_price - open_price) / open_price
' c* o. s) w1 k& J
8 i, ]/ Z% h& a return np.column_stack((frac_change, frac_high, frac_low)),frac_change, frac_high, frac_low3. 模型建立与状态解释2 V7 q; U7 j5 i$ T. R& n) m
我们假设每个隐性状态对应的显性状态都是正态分布的,再初步估计市场一共有5个状态: ' T3 @( H% X7 R2 Q/ m( p: P( ]4 n
_states = 5
9 V& \( _7 [. t' mtrain_data, test_data = train_test_split(df, test_size=0.1, shuffle=False)
- p5 F x: |; s y$ L' K& Q1 J2 Z J" Xfeatures, frac_change, frac_high, frac_low = _extract_features(train_data)0 f. i' _$ T; f$ K" `; ~
model = GaussianHMM(n_components=_states)
. z- ~9 k0 `2 s- q
- n* c" [6 }, D/ e: c8 S3 t0 o% dmodel.fit(features)
! ~- P) y+ V: ]) v- S7 Y- w; x* K; `& `7 e G$ I- r
## GaussianHMM" N/ O D! C8 W- M& Y) ~# O
print("隐藏状态的个数:", model.n_components)
6 v- i0 S8 G+ N! u, q0 Iprint("状态转移矩阵")4 ^7 H1 r) q9 ~# c1 y' O
print(model.transmat_)2 L/ d5 R" n* C i
print("均值矩阵")5 ~9 o% h# p1 C$ z0 \% c7 w n9 q
print(model.means_)
5 [6 o4 P8 U% rprint("方差矩阵")
& n! Y/ u' M* n. E8 I Lprint(model.covars_)
7 ~8 C& V1 x& W8 H, ]& j5 g; \2 i; X9 Q/ W
trans_mat = model.transmat_" g6 B2 C: j5 D! `
means_mat = model.means_
# p$ ~# i6 C4 l& \& [( v2 y5 O; t$ k' E# Ccovar_mat = model.covars_其中trans_mat为隐性状态转移概率矩阵,means_mat为每个隐性状态对应均值矩阵,cover_mat为每个隐性状态对应方差矩阵。
8 r9 _* ]/ I. D ^; ?# H `, j结果如下: , j; P5 v0 n0 C+ \! O) |) n
隐藏状态的个数: 5$ q2 j# o1 _, X: b1 `0 R
$ @" H5 W+ V3 A5 Y! z5 l% B状态转移矩阵& L4 s8 {; O C) J# F
[[4.92841919e-01 3.94296981e-02 4.88723685e-02 4.18168766e-01
' h3 K4 n7 U. A" S4 n+ U 6.87248292e-04]& ]9 J/ c" i V$ v( Q3 |# K
[1.22888498e-01 3.54667807e-01 4.04748939e-01 7.50435445e-027 _$ a7 b( w7 x" g3 A! a
4.26512115e-02]' _0 f8 K8 b2 |* a3 L& I6 \9 u. X
[1.20944857e-01 3.16391469e-01 3.37760871e-01 1.97331090e-01) K; f# }& Y; N$ g, j
2.75717137e-02]
5 f# U' U+ V# J0 i [5.02057408e-01 6.09745059e-02 5.49501647e-02 3.80524622e-01
4 n1 W8 J/ ^1 Y5 u 1.49329942e-03] i4 y& ]7 ~6 o8 |! x; \8 {
[5.46560440e-07 1.66771635e-01 2.20357886e-01 1.45143404e-06
8 a; s$ m& M m- Q' b' m 6.12868481e-01]]5 D% F7 ]/ h- B
; u$ ?* G0 }/ u均值矩阵( t- c' S0 j0 ~% |; m) k
[[ 0.00100483 0.00200838 -0.00069315]- f. ?3 B& S! {" d
[-0.0042892 0.00139075 -0.00662071]
* H, u' q( G+ u3 Y3 l [ 0.00430167 0.00626541 -0.00129704]
2 u- ?# f, m% X' B1 C, l [-0.00127088 0.00068099 -0.0023776 ]# A9 b3 l. _ R% q9 H9 x
[-0.0002794 0.01021583 -0.01188547]]
( {* g9 U9 x' Z# O. y: t& p- s p: z- u3 l, }4 A$ Y- i! E4 [
方差矩阵4 \' X; Q1 i" _
[[[1.78831746e-06 0.00000000e+00 0.00000000e+00]7 M% g; L, l+ G8 q: o. \
[0.00000000e+00 1.79026813e-06 0.00000000e+00]
, F+ O$ y* Q) y7 C( c7 u [0.00000000e+00 0.00000000e+00 7.92414902e-07]]
, p: X& g9 O' M0 _9 Y/ S6 i( E/ Z
9 C! ]6 o5 ?! x, v$ h [[9.22402278e-06 0.00000000e+00 0.00000000e+00]
0 d& N/ {; C2 B ^ [0.00000000e+00 3.06631445e-06 0.00000000e+00] J1 v: G8 K% h& `0 i
[0.00000000e+00 0.00000000e+00 8.07040990e-06]]) C7 M/ ~( ^( y8 }
9 P+ @* O& j5 X1 [4 B9 I
[[8.66631732e-06 0.00000000e+00 0.00000000e+00]
) B1 p4 a/ q/ }+ V2 E7 I3 S [0.00000000e+00 6.85396774e-06 0.00000000e+00]
+ N, y; `' Q! M; K [0.00000000e+00 0.00000000e+00 3.04307130e-06]]
0 J- [: M N: P$ |8 _: @- N- x$ A% f1 K- ?3 F$ S7 `
[[1.90478192e-06 0.00000000e+00 0.00000000e+00]8 A1 O8 D6 V; r; A4 H
[0.00000000e+00 8.76364129e-07 0.00000000e+00]
2 w1 G' l z6 e [0.00000000e+00 0.00000000e+00 1.96545207e-06]] j! j# m2 B' e9 j8 _5 v
2 O" H" j: c( X4 e9 y+ J q
[[2.98827765e-04 0.00000000e+00 0.00000000e+00]) u4 ~0 }" p& U- E6 m2 O& H* a- y
[0.00000000e+00 2.25462090e-04 0.00000000e+00]4 Y7 U. U5 k, }6 z2 G0 k% z
[0.00000000e+00 0.00000000e+00 2.71001164e-04]]]通过均值矩阵可以大概判断分别是怎么样的五个状态:! m3 @1 |/ `* D: N, |- l- S2 }/ q
: I( z* ]& s1 ]3 u6 d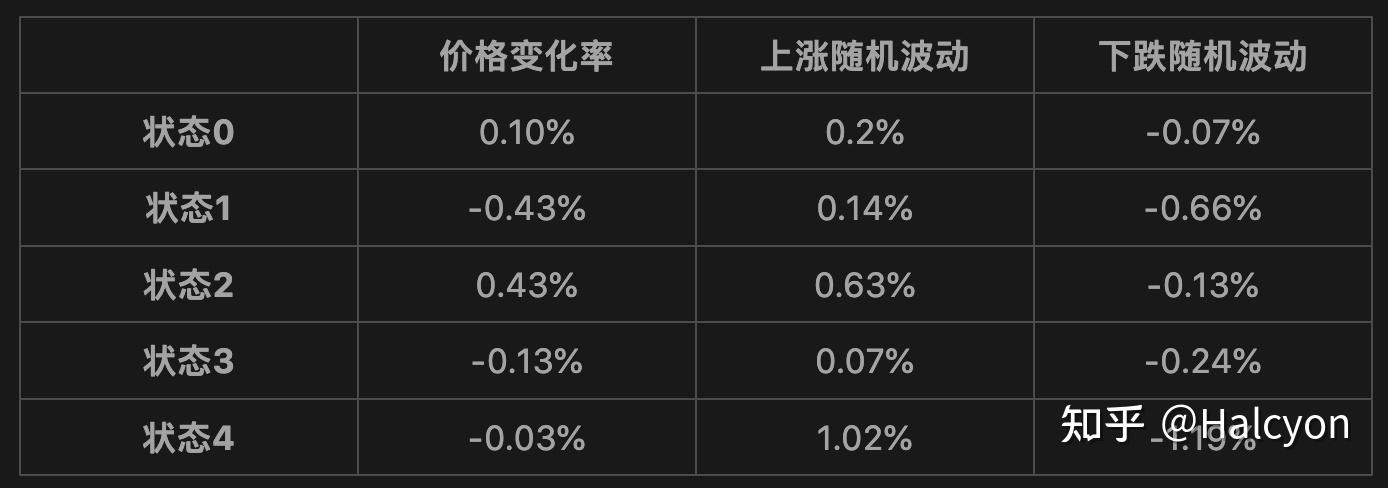
+ \0 A0 l+ Q9 |通过均值矩阵可以大致将以上几种状态分别归类为(对应状态0-4):震荡向上、跌得飞起、涨得飞起、震荡向下、上下乱抖。
* \( l T, v) H+ P, R* f. D为了证明上述分类准确性,查看一下训练集分类的价格波动分布:
5 ~, E! ?6 n5 @plt.figure(figsize=(15,10))
, [! i; s% g' s5 d( `for i in tqdm(range(_states)):
3 i, G7 \# X8 k6 F2 D idx = (decode == i)
% M7 e/ t9 A$ {2 [! p# \5 z! z plt.plot_date(train_data['开盘时间_'].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S"))[idx],frac_change[idx],'.',label='%dth hidden state'%i,lw=0.5)) }( G2 S* G6 i: w/ g9 w# }
plt.legend()& n: `0 W0 U' O, D# ]) @- E. u
plt.grid(1)
* _2 g8 O# K+ D l. Q; ?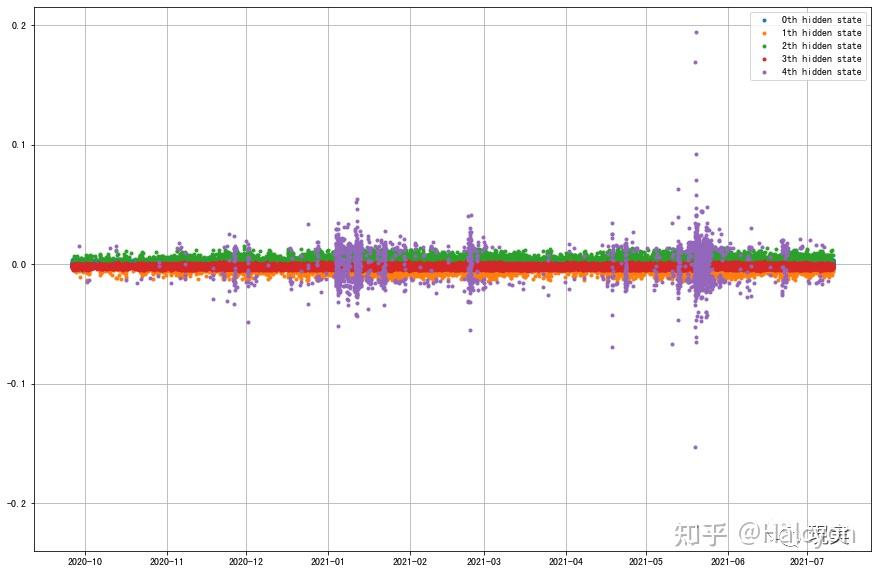 ) m9 V6 O/ d3 x2 M7 j6 ? ) m9 V6 O/ d3 x2 M7 j6 ?
(中间颜色看起来好像汉堡王啊 =_= 饿了)
1 z* g. o, {+ b6 K, z2 G( o
$ f. {) n7 ?, h3 c5 a0 j5 i8 _* h$ u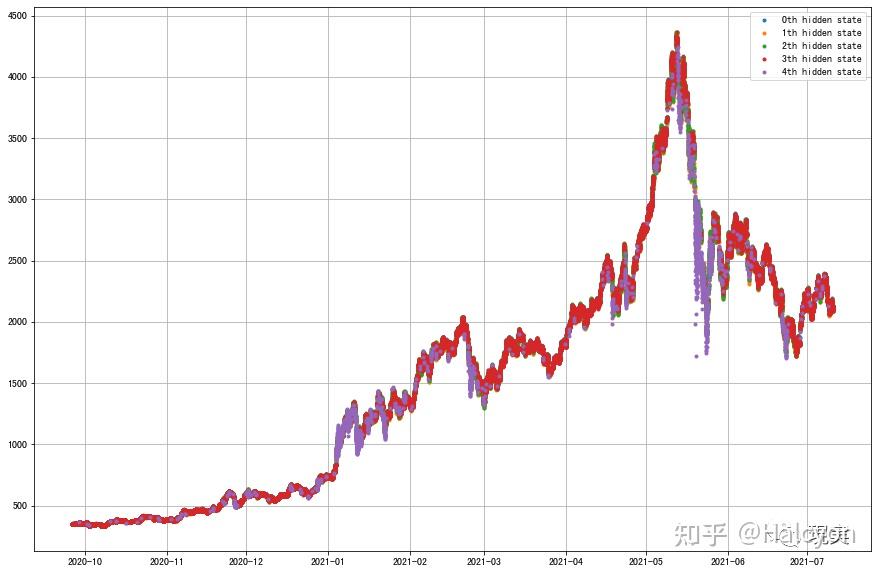
7 ~+ z6 I4 u4 [+ H. y3 N X8 J1 \! {/ j通过波动分布感觉分类较为准确,下面观察一下各个状态的转移概率矩阵:8 t1 l% F. {6 y
m: ~: o0 c* `- ~8 P4 Q8 O% `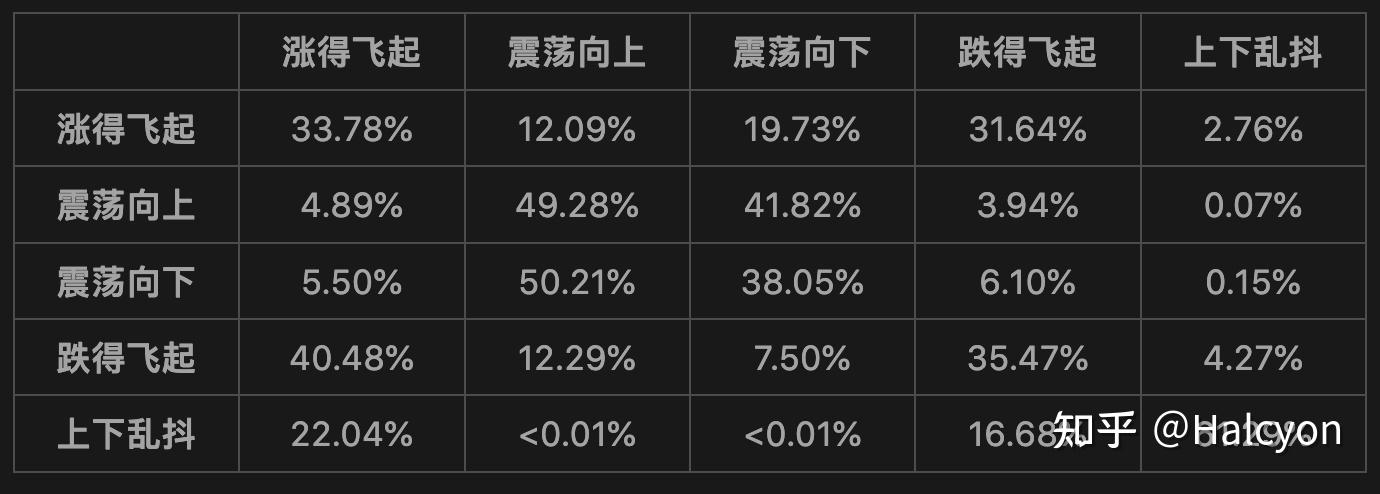 9 |6 m$ N: L6 w( X% f) u 9 |6 m$ N: L6 w( X% f) u
显性分布也较为符合认知。 3 S1 Z1 y `8 ?7 F! V0 Y3 b; w
4. 显性状态分布( O. B" N" r, ?7 ]+ A$ E. w
知道了隐性状态的转移概率后,下面可以分别观察每个隐性状态对应的显性状态(每个bar的价格变化比例)的分布:
! j/ c5 ^9 R6 ^; H! t6 U" n- C$ [8 l! i
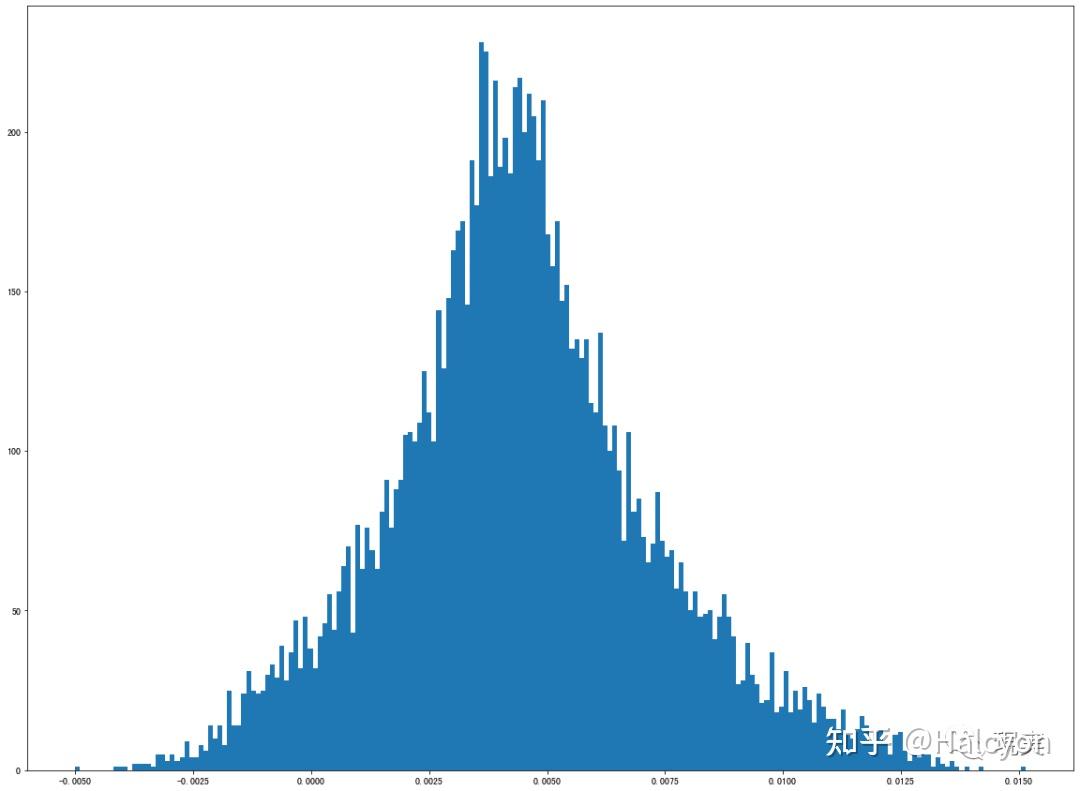
3 z! k. O2 [8 I8 j! U4 \% M6 ]+ Y, Z9 {% M& j: d
涨得飞起& B( Y5 U$ U# ^
9 ?( L V, ^/ {! [6 @9 h6 u; B
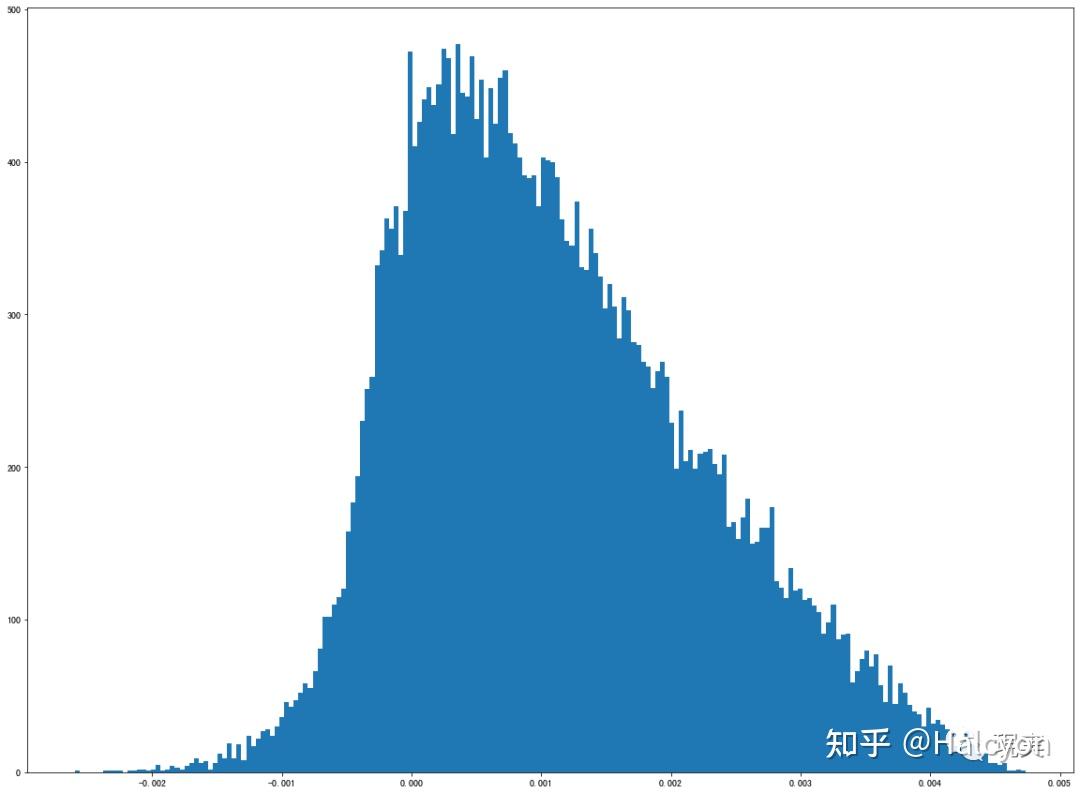
6 i; m3 h3 g( z7 ^
' N! e P) c( M震荡向上) k+ |' Y: u: J" ~
( G! V" T% s6 }8 q+ G7 v
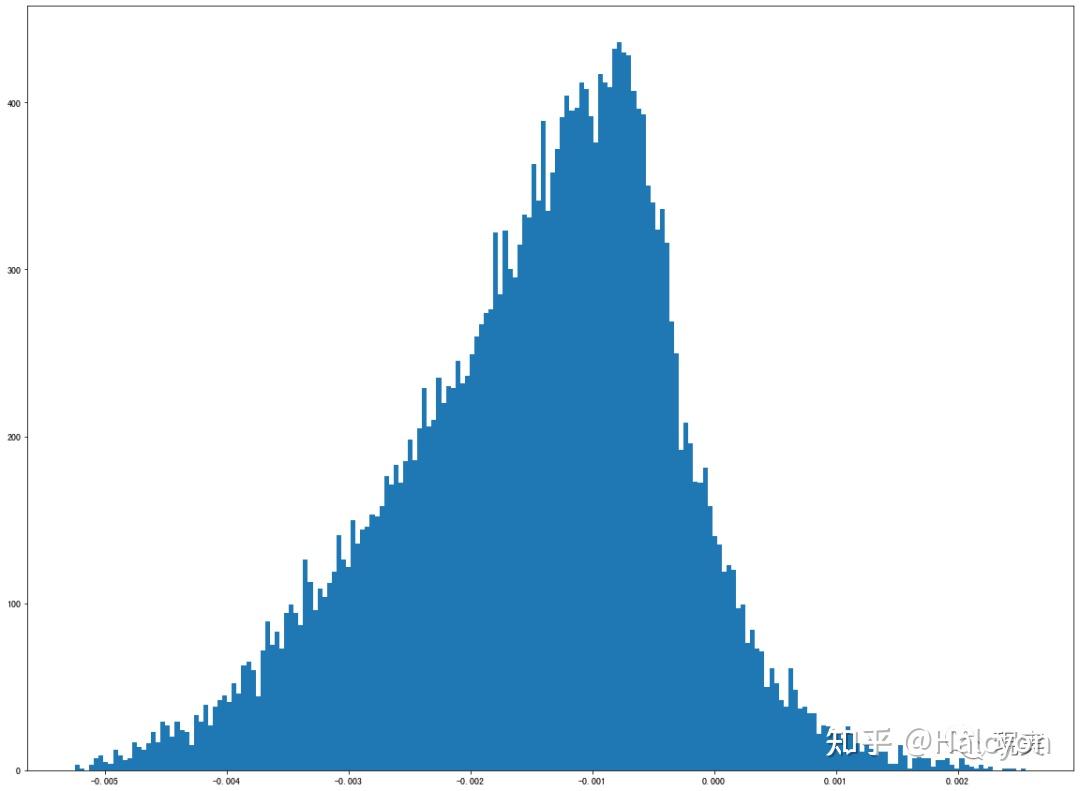
9 M5 o' z1 [- C6 e5 j$ v5 G
5 k4 \4 A! u0 O& _, Z0 k震荡向下" I$ b+ ]3 \3 _# v W* E" n0 D
4 T6 S* X2 o- A) {, B5 V
8 N2 _: M' k9 o/ G8 \' M6 D) c0 x' W' l0 [1 g. T4 _
跌得飞起
# q1 i+ w" w' q$ h2 I# K9 ~- }5 P) B5 ^! ~1 P) h& z+ K6 J' ]
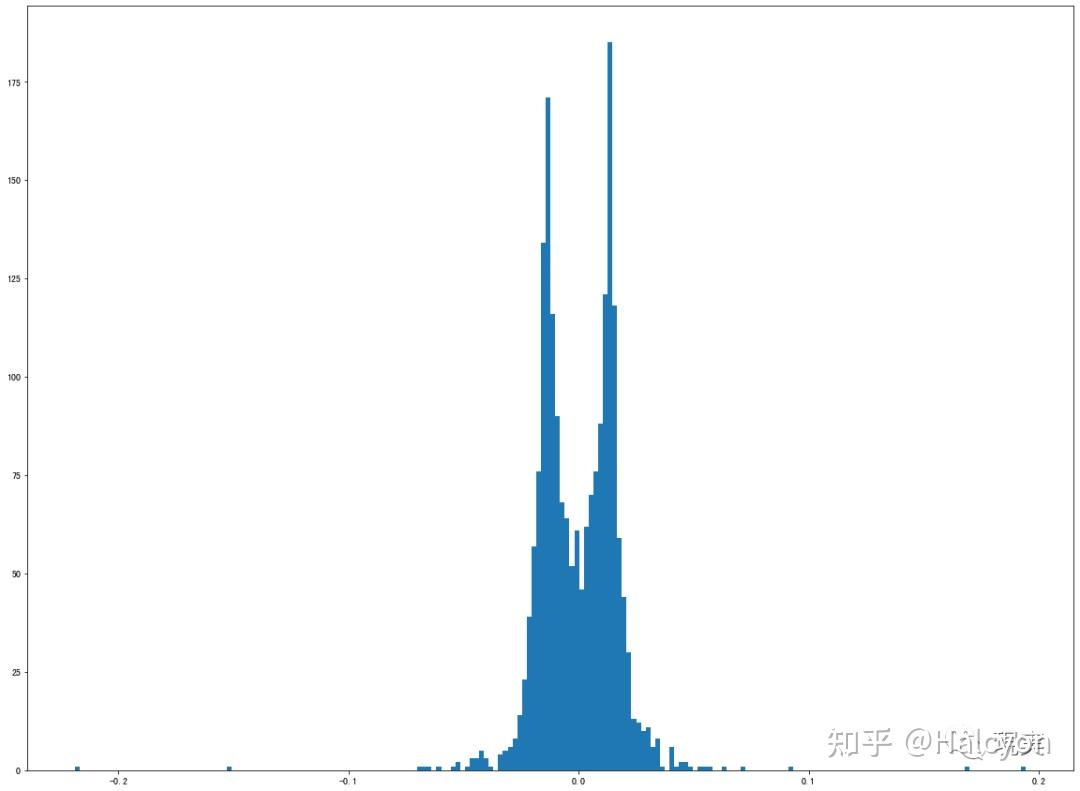
X1 A8 O- D& v( Q! A6 F3 V6 w
; h; r; j. Y& h) h. T: t6 U/ D [上下乱抖
0 G4 [# U) o9 K
0 m. q _- A# L2 @9 q) H7 R% a观察到涨得飞起和跌得飞起都是高峰度的正态分布,而震荡向上和震荡向下都是明显有偏的偏态分布,上下乱抖则有两个尖峰,且非常薄尾。
+ @6 e8 d7 O: c0 k# M通过以上几个显性状态的分布可以更精确的进行抽样。
. F' N; |: [3 u3 B) i9 E" F5. 蒙特卡洛模拟
D" L/ O( L8 d$ I, D1 H最后使用测试集来进行隐性状态转移模拟和对比,我们对接下来的100个时间戳进行蒙特卡洛模拟,以训练集的最后一个时间戳的状态为起始状态,模拟10000次,再从训练集的显性分布中进行对应抽样(这里我的抽样逻辑不太严谨,是假设的正态分布进行的抽样,实际上可以进行分布拟合再进行抽样或者直接从原数据中进行抽样都会更好一些),观察上下三个sigma之间的模拟结果:* G) a+ }. a2 |* I
def simulation(init_state,_states,num_simulations,periods,trans_mat,means_mat,covar_mat):0 h* `$ u6 E3 q8 }, E
states = [i for i in range(_states)]
. W8 e3 i5 w+ e- H4 U7 G* b$ M4 U mean_arr = [means_mat[j][0] for j in range(_states)]
( Z8 n% I* G1 k( M0 e8 y8 o sd_arr = [np.sqrt(covar_mat[0][0]) for i in range(_states)]
3 \" w* D: e/ d: O! C
9 o4 Q0 T$ Z( _% Q' ] midline_trend = []3 e$ W/ K1 q' C' B: u5 p) r
up_one_sigma_trend = []
0 f! Y6 z$ T: ?# Z9 P up_two_sigma_trend = []
& I. e8 L& `2 R% `; x up_three_sigma_trend = []$ D, i+ U, Y- Z: R Y/ P7 V
down_one_sigma_trend = []
7 ?& [) p2 d. o1 [ down_two_sigma_trend = []
[2 c ~ I0 A: ~% X- ?5 s, T! m down_three_sigma_trend = []6 c8 D ]3 y2 @) d& I' @& o5 j
sims = []. I/ X3 k6 n- [$ m" @6 M
for j in tqdm(range(num_simulations)):
8 r' H f. |! T sim = [0]*(periods+1)
$ n& v1 T5 D1 B" B3 [: f sim[0] = init_state3 {0 k& X0 g$ V( t( S
#sim[0] = model.decode(features)[1][-1]
, z. v! ~, U1 q6 d trans_df = pd.DataFrame(trans_mat)" p; v% t3 m% \$ B
for i in np.arange(1,periods+1):
2 C) }* R! s. h sim = np.random.choice(states, 1, p = trans_df.loc[sim[i-1],:])[0]$ o# ?( k) g4 c# z
sim = sim[1:]. n6 R y* _, } N A4 @
sims.append(sim)
_8 J' e4 m. @5 S' Y' w, m8 w. e3 F* v! ]
midline_trend.append([mean_arr[sim] for i in range(periods)])
* r$ P, {' U2 ~4 x+ C! b4 e up_one_sigma_trend.append([mean_arr[sim]+1*sd_arr[sim] for i in range(periods)])( U) ^. i& K( x' _* y M1 ~
up_two_sigma_trend.append([mean_arr[sim]+2*sd_arr[sim] for i in range(periods)])* b3 f6 v( G5 D/ w
up_three_sigma_trend.append([mean_arr[sim]+3*sd_arr[sim] for i in range(periods)])6 R1 R$ p% l4 n8 i9 o# K
down_one_sigma_trend.append([mean_arr[sim]-1*sd_arr[sim] for i in range(periods)])( K* Y' n1 k* X$ W1 W
down_two_sigma_trend.append([mean_arr[sim]-2*sd_arr[sim] for i in range(periods)])4 [! Z% ~4 a+ Z! U! s8 ]( l3 Z
down_three_sigma_trend.append([mean_arr[sim]-3*sd_arr[sim] for i in range(periods)])
. ?. }7 H8 i/ R2 Y* ]9 {2 ^ " P/ }# h' V& C) E2 m7 b. y/ O
sims = pd.DataFrame(sims).mode()
0 Y8 I7 Z5 p9 p/ [* A+ d6 F7 I4 B midline_trend = pd.DataFrame(midline_trend).mean()- j6 Q0 ~9 \2 l& K" T
up_one_sigma_trend = pd.DataFrame(up_one_sigma_trend).mean()/ v+ u) E* ?$ S, y; P5 G3 q
up_two_sigma_trend = pd.DataFrame(up_two_sigma_trend).mean()
?! u5 s2 G0 m4 M7 z up_three_sigma_trend = pd.DataFrame(up_three_sigma_trend).mean(), X* r/ A( O/ s0 T9 b& f$ o
down_one_sigma_trend = pd.DataFrame(down_one_sigma_trend).mean()( d( R# H! j) S3 }" _/ A* E. m
down_two_sigma_trend = pd.DataFrame(down_two_sigma_trend).mean()( I2 k+ I" U, g4 T2 u' E
down_three_sigma_trend = pd.DataFrame(down_three_sigma_trend).mean(): x7 z# z, M$ s0 K, E: ]# k1 L5 U* K
4 Z- N, x8 g. K! ]9 J; b return sims,midline_trend,up_one_sigma_trend,up_two_sigma_trend,up_three_sigma_trend,down_one_sigma_trend,down_two_sigma_trend,down_three_sigma_trendsims,midline_trend,up_one_sigma_trend,up_two_sigma_trend,up_three_sigma_trend,down_one_sigma_trend,down_two_sigma_trend,down_three_sigma_trend = simulation(model.decode(features)[1][-1],_states,10000,100,trans_mat,means_mat,covar_mat)! v! `1 M$ }" B6 ~( \
test_data = test_data.reset_index(drop=True) P: R& s2 H# ?4 R3 i! U
frac_change_test = _extract_features(test_data)[1][:100]7 V Z" w) ]" R) C5 C
frac_high_test = _extract_features(test_data)[2][:100]- T8 G, D9 V" N; y& }) }7 v
frac_low_test = _extract_features(test_data)[3][:100]/ t& c1 D4 R. f7 F" y
: g& J9 P. D/ A; r
def get_values(arr):" W9 U$ s y+ N0 Z5 R
result = []
0 M3 y8 x* x0 K8 A b% `# w for i in range(len(arr)):
U$ V; u; }! f" h if i == 0:
8 I7 V% s$ L. @# H result.append(1*(1+arr[0]))
4 T2 R; n; P7 ` else:/ x. u) F; k% D8 ?) e
result.append(result[i-1]*(1+arr))! ~) z9 |) i4 I' Z# m
return result
9 ~) B9 p# B3 L
( p% l8 t* L8 q( oplt.figure(figsize=(15,10))! w0 P7 E _ y4 w
plt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),frac_change_test,'-',label='close',lw=1)1 Y7 L& d+ k+ ^# b/ g1 C
plt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),frac_high_test,'-',label='high',lw=1)
5 V; {0 j- H h& ^- I$ X ^5 pplt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),frac_low_test,'-',label='low',lw=1)
/ G& m' j7 ~" ]1 `plt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),midline_trend,'-',label='midline',lw=0.5)3 l! Y2 S' A* G
plt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),up_one_sigma_trend,'-',label='up-1-sigma',lw=0.5)
5 ?6 j. x: b! E z% xplt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),up_two_sigma_trend,'-',label='up-2-sigma',lw=0.5)0 k( F( D a) N o [9 Q. {7 ]" G
plt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),up_three_sigma_trend,'-',label='up-3-sigma',lw=0.5)
) N0 W. B" A% ^plt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),down_one_sigma_trend,'-',label='down-1-sigma',lw=0.5)
' M) I1 L4 J N Vplt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),down_two_sigma_trend,'-',label='down-2-sigma',lw=0.5)
) [% y; X/ o3 L7 e$ Kplt.plot_date(test_data['开盘时间_'][:100].apply(lambda x:datetime.datetime.strptime(x, "%Y-%m-%d %H:%M:%S")),down_three_sigma_trend,'-',label='down-3-sigma',lw=0.5)* o( J0 p: {# ~, w X
plt.legend()结果如下:
& R& l: \& E2 F5 X# y3 p
; \7 O; i7 q3 l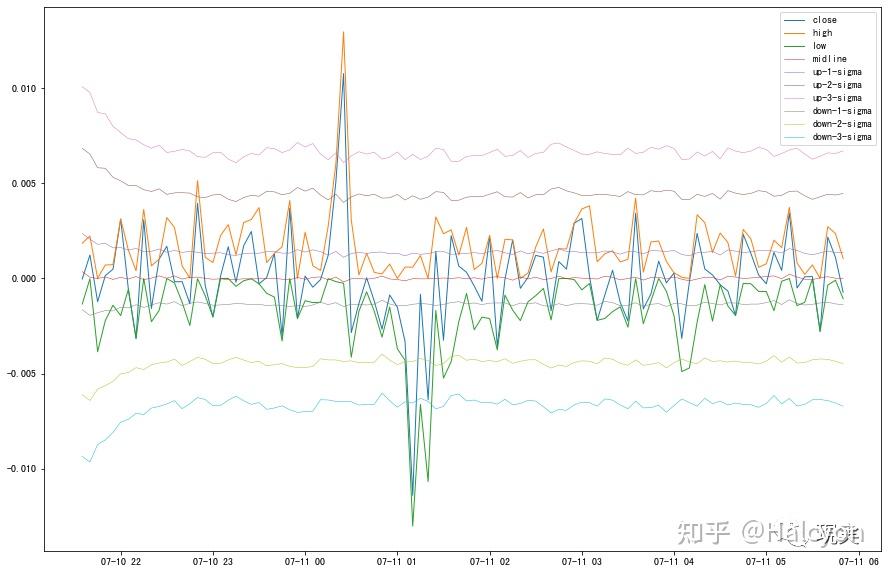 0 Q* b$ Q, ]0 t/ ? 0 Q* b$ Q, ]0 t/ ?
可以看出来大部分5min波动都在两个sigma之内,不过关于实际应用还没有想到有什么可以比较好利用这个点的方式,可以作为未来探索方向。 . n6 O* j: c1 s; U" O% N4 n
<hr/>6. 小结和Future Works+ k, c, i- w- o R, r; v
, ]! o5 @: b3 \8 j0 ~0 m

$ U1 U" J. }9 ?6 W4 }( B9 { m5 u$ u0 U虽然通过这种方式可以从另一个角度解读价格走势的变化,但是实际应用上还有所欠缺,目前做的这些研究工作还是比较碎片化,下次再做HMM的探索时希望可以沉淀一些策略层面上的东西。
. t: u% ]- N: C. F |3 n7 K一些Future Works:
6 d- Z* Y3 P% E% |: W2 c2 o- r1 Z4 I* F* Q
- 使用价格的对数变化率替代绝对变化率;2 `* U9 s% n* L
- 显性状态抽样优化,可以使用拟合后的分布进行抽样;
( u0 s) ~& _) m2 {8 f - 使用更丰富的隐性状态来解释价格走势状态;
; ]! @# l, N- a) m; a - 探索隐性状态转移在策略层面上的应用。/ f9 U2 p& Z7 n' k6 [
此外,对于HMM的应用层面如果有任何想法欢迎留言交流~
: B1 S; C7 [. Y+ o# t2 @0 Q谢谢大嘎!# t! y6 o8 h+ B4 C2 A
附:前几次的文章
2 }' |1 Y" p# W) ~& u. l" C加密货币衍生品实战日记(八)—— 币本位溢价与资费套利策略详解 ( L! C5 a" ~- K# r0 E" l
加密货币衍生品实战日记(七)——蒙特卡洛在价格走势范围预测上的应用(译)
4 e( T6 K* z7 k$ f; D$ L4 k5 q加密货币衍生品实战日记(六)——隐马尔科夫链对于状态的预测 ; l- _: W6 p3 Q3 R S+ ~& k4 i
<hr/>
8 T' ]! G$ Q F7 p |