贝叶斯定理太有用了,不管是在投资领域,还是机器学习,或是日常生活中几乎都在用到它。
( d; ], B3 e, u7 [例如,生命科学家用贝叶斯定理研究基因是如何被控制的;教育学家意识到,学生的学习过程其实就是贝叶斯法则的运用;基金经理用贝叶斯法则找到投资策略;谷歌用贝叶斯定理改进搜索功能,帮助用户过滤垃圾邮件;无人驾驶汽车接收车顶传感器收集到的路况和交通数据,运用贝叶斯定理更新从地图上获得的信息;人工智能、机器翻译中大量用到贝叶斯定理...% t$ R7 I' Y0 v7 E p
% y5 A& Y$ ? \
我将从以下4个角度来科普贝叶斯定理及其背后的思维:4 Z+ R x& E& H
1.贝叶斯定理有什么用?' m) @" w- [- O. e8 e
2.什么是贝叶斯定理?% B+ d/ ]: e& E4 f0 V
3.贝叶斯定理的应用案例
8 n, ]' {1 k- \' S# B( W. z4.生活中的贝叶斯思维
( ^ K8 q; O1 r& {4 z
5 x( u" x& g! V. u7 A% Y' b! H1.贝叶斯定理有什么用? 英国数学家托马斯·贝叶斯(Thomas Bayes)在1763年发表的一篇论文中,首先提出了这个定理。而这篇论文是在他死后才由他的一位朋友发表出来的。4 X' L/ H3 R7 u. {
(ps:贝叶斯定理其实就是下面图片中的概率公式,这里先不讲这个公式,而是重点关注它的使用价值,因为只有理解了它的应用意义,你才会更有兴趣去学习它。)
4 |) j* v- G( c; U# u, S+ n8 G' l7 ~& H/ [% e* V/ ~8 d- c
 " K8 L s2 o4 R' ~ " K8 L s2 o4 R' ~
在这篇论文中,他为了解决一个“逆概率”问题,而提出了贝叶斯定理。9 }$ U+ @& k- t& M' B" f
在贝叶斯写这篇文章之前,人们已经能够计算“正向概率”。什么是正向概率呢?举个例子,杜蕾斯举办了一个抽奖,抽奖桶里有10个球,其中2个白球,8个黑球,抽到白球就算你中奖。你伸手进去随便摸出1颗球,摸出是中奖球的概率是多大。* ?* n/ ^" O8 e2 d6 p
4 e7 N/ a3 X5 K- W0 u5 s; [7 M
9 j% L! C$ i2 n根据频率概率的计算公式,你可以轻松的知道中奖的概率=中奖球数(2个白球)/球总数(2个白球+8个黑球)=2/10) h% k& q! X: f v
如果还不懂怎么算出来的,可以看我之前写的科普概率的回答:猴子:如何理解条件概率?
* Z& P) S7 _) u( ? Q, f% c; p9 f4 j
而贝叶斯在他的文章中是为了解决一个“逆概率”的问题。比如上面的例子我们并不知道抽奖桶里有什么,而是摸出一个球,通过观察这个球的颜色,来预测这个桶里里白色球和黑色球的比例。% y# b n& D/ T1 [! c- E
* r3 {5 p3 _2 s$ r. d+ X" E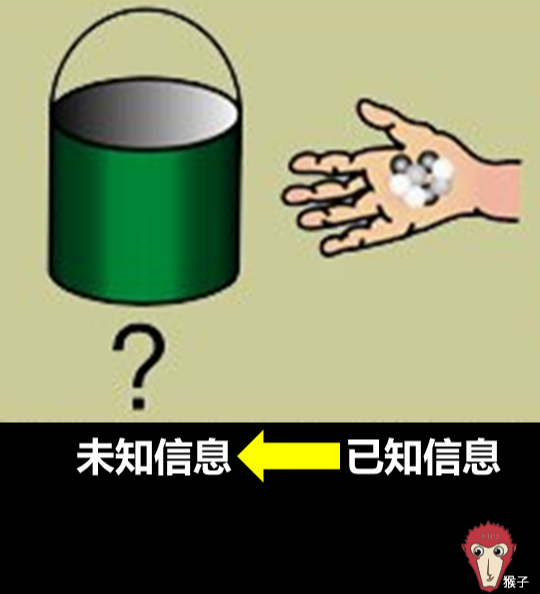
- N$ z$ ^# f+ z& c这个预测其实就可以用贝叶斯定理来做。贝叶斯当时的论文只是对“逆概率”这个问题的求解尝试,这哥们当时并不清楚这里面这里面包含着的深刻思想。' p# N9 |9 x' \# q" C+ v$ F( p, c) z
# f9 U- P+ M( ^) e. f' W k
然而后来,贝叶斯定理席卷了概率论,并将应用延伸到各个领域。可以说,所有需要作出概率预测的地方都可以见到贝叶斯定理的影子,特别地,贝叶斯是机器学习的核心方法之一。( W5 _0 c7 N* Z
' K& b" ?; ^, N, B6 P
为什么贝叶斯定理在现实生活中这么有用呢?4 l4 X8 q7 B2 I
这是因为现实生活中的问题,大部分都是像上面的“逆概率”问题。因为生活中绝大多数决策面临的信息都是不全的,我们手中只有有限的信息。既然无法得到全面的信息,我们就只能在信息有限的情况下,尽可能做出一个好的预测。1 a8 g4 q( C' J, G% {+ y
比如天气预报说,明天降雨的概率是30%,这是什么意思呢?
" B) V2 S) E9 M1 Y6 u7 V2 @我们无法像计算频率概率那样,重复地把明天过上100次,然后计算出大约有30次会下雨(下雨的天数/总天数)
S+ K& \6 a3 r而是只能利用有限的信息(过去天气的测量数据),用贝叶斯定理来预测出明天下雨的概率是多少。
0 M' X% ~6 a/ v+ D+ B' x4 n4 l9 G( J4 t+ ~; u# U
同样的,在现实世界中,我们每个人都需要预测。想要深入分析未来、思考是否买股票、政策给自己带来哪些机遇、提出新产品构想,或者只是计划一周的饭菜。0 ^* y. f9 @" r+ g! r1 s% N
- W" F) ?9 v& @: {+ u贝叶斯定理就是为了解决这些问题而诞生的,它可以根据过去的数据来预测出未来事情发生概率。
# [' q6 y7 z R- w% n, Y/ v' w% M! b) [0 A% d
贝叶斯定理的思考方式为我们提供了有效的方法来帮助我们做决策,以便更好地预测未来的商业、金融、以及日常生活。
7 t. `5 q1 D7 q7 S% N3 r
& p% H' G5 Y& |总结下第1部分:贝叶斯定理有什么用?+ c' X/ B; d$ v+ x
在有限的信息下,能够帮助我们预测出概率。
7 R! M: P. M% w& q$ i8 [所有需要作出概率预测的地方都可以见到贝叶斯定理的影子,特别地,贝叶斯是机器学习的核心方法之一。例如垃圾邮件过滤,中文分词,艾滋病检查,肝癌检查等。( R$ c0 y0 v# b s+ i y+ _' R
( s) Q6 Q5 v" p' m3 _) q" `
2.什么是贝叶斯定理? 贝叶斯定理长这样:
$ {. J4 S, p u, t0 k/ o6 r. z$ n& r
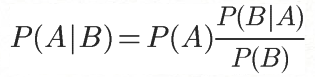
$ w6 I8 T5 r2 V4 V/ F2 Q到这来,你可能会说:猴子,说人话,我一看到公式就头大啊。
4 c( H3 p0 e v1 F+ H2 P( h- S其实,我和你一样,不喜欢公式。我们还是从一个例子开始聊起。
: w; G8 X" ~( F* q9 ]5 V- v+ O% x7 h/ G4 E! z1 A! e: i ~8 S. X6 c
我的朋友小鹿说,他的女神每次看到他的时候都冲他笑,他现在想知道女神是不是喜欢他呢?
' z0 ^4 _: C4 p5 n谁让我学过统计概率知识呢,下面我们一起用贝叶斯帮小鹿预测下女神喜欢他的概率有多大,这样小鹿就可以根据概率的大小来决定是否要表白女神。
8 j: v0 K& ?% a2 V5 f' ?! A" O5 m首先,我分析了给定的已知信息和未知信息:
9 ]7 l( R& K! z2 @. X& ^1)要求解的问题:女神喜欢你,记为A事件 t% j2 z$ E; H! {8 @
2)已知条件:女神经常冲你笑,记为B事件8 ^# ~, ]7 F" f1 L9 t! f) h
" r8 ]5 _) O2 F, E. p1 h* Y v所以,P(A|B)表示女神经常冲你笑这个事件(B)发生后,女神喜欢你(A)的概率。* W$ S e' K/ ~- {: X( O
+ h0 Y7 U" Y. @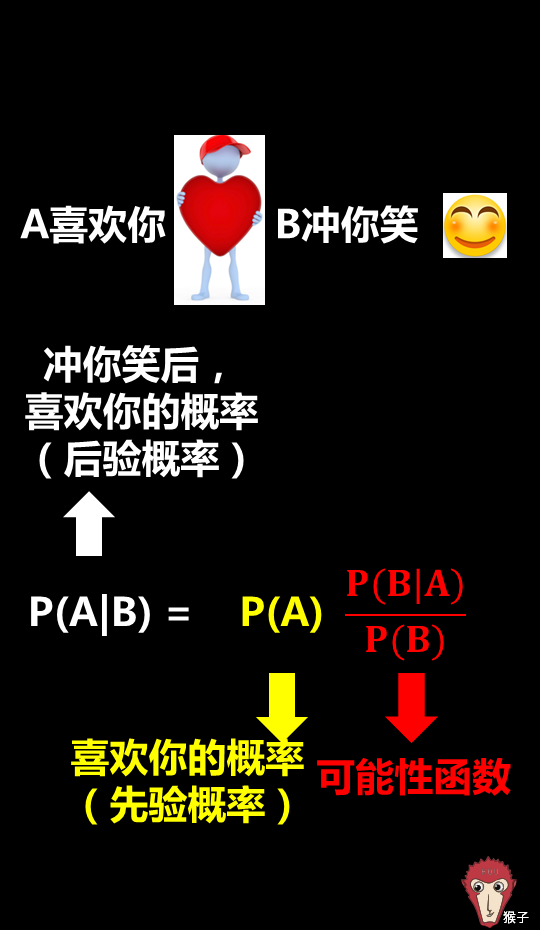 4 t- R( u0 p- z! L 4 t- R( u0 p- z! L
从公式来看,我们需要知道这么3个事情:& G+ E( y0 r2 v9 q" s R V
1)先验概率5 H3 }1 X+ \' o6 v" P+ A N
我们把P(A)称为"先验概率"(Prior probability),也就是在不知道B事件的前提下,我们对A事件概率的一个主观判断。7 J0 h2 u4 E( J" G% l3 B2 n
对应这个例子里就是在不知道女神经常对你笑的前提下,来主观判断出女神喜欢一个人的概率。这里我们假设是50%,也就是不喜欢你,可能不喜欢你的概率都是一半。7 P7 E; }) e' h' r4 G2 P5 @) @/ h e
+ g1 m$ S$ _) T; l
2)可能性函数# k) \/ R% K* i$ G. o1 Q$ ]
P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,也就是新信息B带来的调整,作用是将先验概率(之前的主观判断)调整到更接近真实概率。
- }, t' V! ?* e. u: o( `+ _; i
& I* X8 o S! i9 [* ~可能性函数你可以理解为新信息过来后,对先验概率的一个调整。比如我们刚开始看到“人工智能”这个信息,你有自己的理解(先验概率-主观判断),但是当你学习了一些数据分析,或者看了些这方面的书后(新的信息),然后你根据掌握的最新信息优化了自己之前的理解(可能性函数-调整因子),最后重新理解了“人工智能”这个信息(后验概率) A- P4 X, A% t9 P7 }5 b0 u$ U
( b3 ^' a: j0 P8 o$ |( E( Z
如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;+ H2 h% h8 f% I4 \1 D
如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;
" a, `/ y7 n; m1 p7 r2 ^% h% h$ y3 t如果&#34;可能性函数&#34;<1,意味着&#34;先验概率&#34;被削弱,事件A的可能性变小。
" }2 f9 i6 {2 m/ t. Z4 c) l
3 S, u7 N* D$ C6 L2 c. O# T还是刚才的例子,根据女神经常冲你笑这个新的信息,我调查走访了女神的闺蜜,最后发现女神平日比较高冷,很少对人笑,也就是对你有好感的可能性比较大(可能性函数>1)。所以我估计出&#34;可能性函数&#34;P(B|A)/P(B)=1.5(具体如何估计,省去1万字,后面会有更详细科学的例子)
: ~9 M& z6 x- Y$ @ x' H( _( s( e4 {5 j% x2 Y- N* U/ M
3)后验概率+ G* |" E% W# Y8 r2 X
P(A|B)称为&#34;后验概率&#34;(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。这个例子里就是在女神冲你笑后,对女神喜欢你的概率重新预测。
0 a3 U( D" Z1 O3 o' C+ x/ Z) n带入贝叶斯公式计算出P(A|B)=P(A)* P(B|A)/P(B)=50% *1.5=75%9 U8 v3 ]2 A1 F) L; O2 {" m6 ^& ]
6 y8 ^1 d) c& A; r# b1 H因此,女神经常冲你笑,喜欢上你的概率是75%。这说明,女神经常冲你笑这个新信息的推断能力很强,将50%的&#34;先验概率&#34;一下子提高到了75%的&#34;后验概率&#34;。
) N% I3 u$ Z- t7 w1 j' Z. f
& n9 A5 R( {/ G* ?) z4 c1 z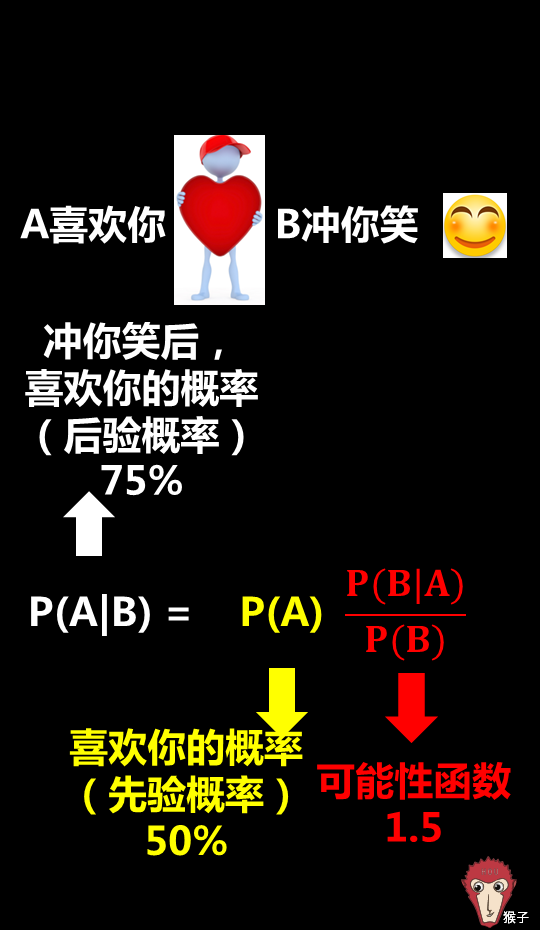 4 U# J w+ N6 F2 l- W+ ^4 \ 4 U# J w+ N6 F2 l- W+ ^4 \
在得到概率值后,小鹿自信满满的发了下面的表白微博:9 B5 R W& a5 O
9 q: S. T$ U4 p2 H1 A 4 A( K3 l4 I2 H, \- u* j 4 A( K3 l4 I2 H, \- u* j
稍后,果然收到了女神的回复。预测成功。& n# w1 }) R) L S2 r- G
) w$ q9 J, ~" N7 k8 s2 @
 " b" [% p f/ T- j4 h$ u! P7 |8 q/ I " b" [% p f/ T- j4 h$ u! P7 |8 q/ I
现在我们再看一遍贝叶斯公式,你现在就能明白这个公式背后的关键思想了:( t, v+ d! e1 _7 u; s
我们先根据以往的经验预估一个&#34;先验概率&#34;P(A),然后加入新的信息(实验结果B),这样有了新的信息后,我们对事件A的预测就更加准确。0 i2 g7 s3 h9 x
' `/ T1 c' l+ D+ A3 R W" {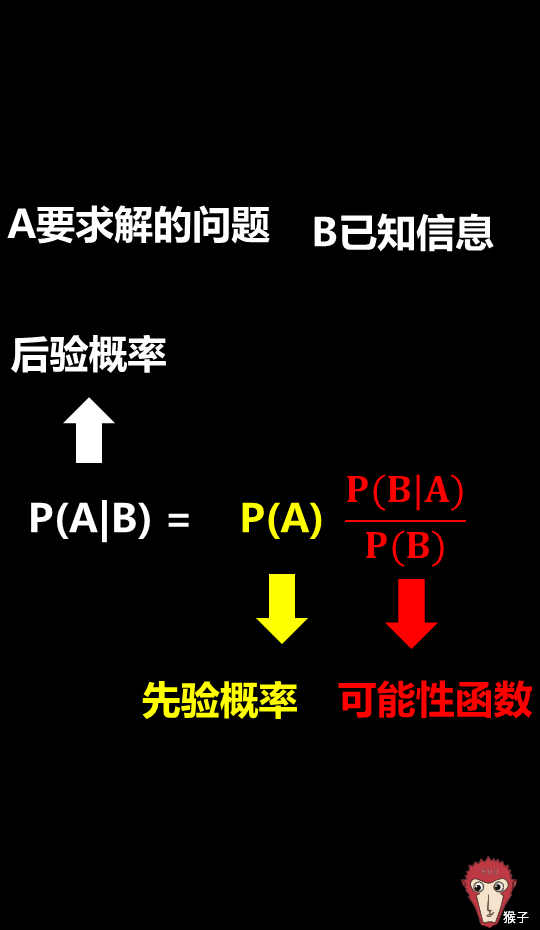
( Z* b9 s5 R7 l5 w因此,贝叶斯定理可以理解成下面的式子:
* L: V9 ^* A2 A2 u) r+ C后验概率(新信息出现后的A概率) = 先验概率(A概率) x 可能性函数(新信息带来的调整)
% l- ]. u0 [1 a9 i& e. f' x7 O贝叶斯的底层思想就是:7 E# G5 f7 \6 }- j* n: K" Z$ S) w5 Q
如果我能掌握一个事情的全部信息,我当然能计算出一个客观概率(古典概率)。
7 {9 [, e7 e5 x3 \/ m$ S/ D* D9 b- s" K可是生活中绝大多数决策面临的信息都是不全的,我们手中只有有限的信息。既然无法得到全面的信息,我们就在信息有限的情况下,尽可能做出一个好的预测。也就是,在主观判断的基础上,你可以先估计一个值(先验概率),然后根据观察的新信息不断修正(可能性函数)。
% y3 ^9 E$ X) `( \2 B4 Z如果用图形表示就是这样的:
* K2 P' S6 t9 z& U* v& P4 v0 j2 V9 y! f. Z; N& \2 ?) A
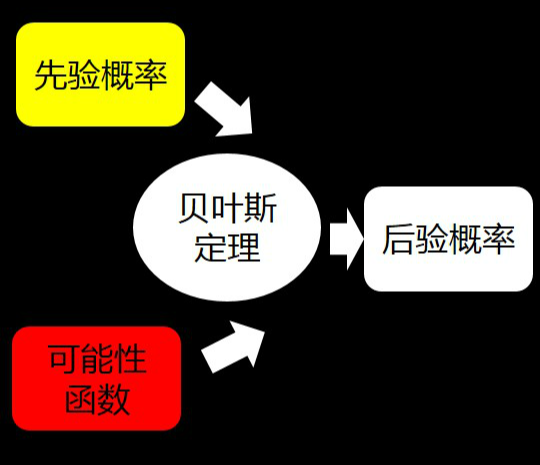 . S7 `1 J% P" ~3 F' M' P . S7 `1 J% P" ~3 F' M' P
其实阿尔法狗也是这么战胜人类的,简单来说,阿尔法狗会在下每一步棋的时候,都可以计算自己赢棋的最大概率,就是说在每走一步之后,他都可以完全客观冷静的更新自己的概率值,完全不受其他环境影响。0 X \% u! B9 \, Y
0 F2 ]; G# L- q, k/ R3 S* s7 G' h8 F
3.贝叶斯定理的应用案例 前面我们介绍了贝叶斯定理公式,及其背后的思想。现在我们来举个应用案例,你会更加熟悉这个牛瓣的工具。
7 @# e2 R! r& S* n: u& u5 \为了后面的案例计算,我们需要先补充下面这个知识。
H9 c4 W `/ n1 z' }, F1.全概率公式
3 P6 }/ u/ p5 R- L9 T9 ~! @$ ]这个公式的作用是计算贝叶斯定理中的P(B)。# |% }: i2 k5 ]5 B1 W
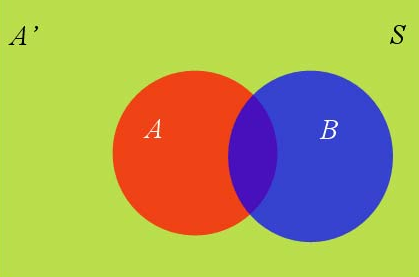
假定样本空间S,由两个事件A与A&#39;组成的和。例如下图中,红色部分是事件A,绿色部分是事件A&#39;,它们共同构成了样本空间S。/ n; M. l5 Q- r8 M3 t+ }
0 k& l) Q/ j. y$ d2 G: M0 l + g+ ]& |9 H: m7 y4 Z5 J + g+ ]& |9 H: m7 y4 Z5 J
这时候来了个事件B,如下图:
; t- y$ |0 Q1 C7 I \" N- E6 z( D8 c- z9 w8 H* m1 {/ Q
6 j& b( J% v: {: Q+ w) p7 z全概率公式:
- Q/ U" E7 t$ a5 w) J1 H
; S1 g* J. `0 f& J/ o% }6 v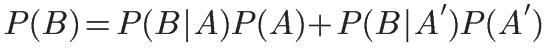
6 z! M) R6 J' F' m+ {9 f它的含义是,如果A和A&#39;构成一个问题的全部(全部的样本空间),那么事件B的概率,就等于A和A&#39;的概率分别乘以B对这两个事件的条件概率之和。
! v5 a; n# G+ Y3 ?7 S6 b
/ @) l# K8 ?* Q, l看到这么复杂的公式,记不住没关系,因为我也记不住,下面用的时候翻到这里来看下就可以了。
8 B& d! h5 H" ]/ K( x( l- t. {$ G+ Z* Q6 h% X
案例1:贝叶斯定理在做判断上的应用
, d; |0 b& A4 ]8 V1 @有两个一模一样的碗,1号碗里有30个巧克力和10个水果糖,2号碗里有20个巧克力和20个水果糖。6 i7 t O4 @* T% |: Q+ {
' G2 q/ n8 M- k. w) U0 P
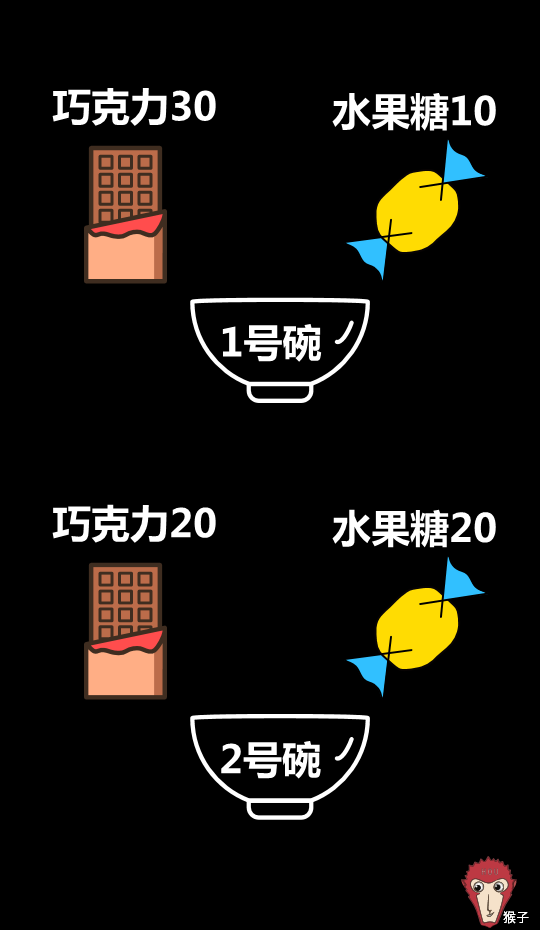
9 r* ~0 v7 ^% S* m( a然后把碗盖住。随机选择一个碗,从里面摸出一个巧克力。$ m, I$ q) n& i: i$ V0 d9 M0 C
问题:这颗巧克力来自1号碗的概率是多少?! T# s8 C; [0 n. S( h, U% x2 k7 i! K
4 ]$ k; h! u) Q6 L( T, [
好了,下面我就用套路来解决这个问题,到最后我会给出这个套路。
7 t0 L8 g! B, s' r3 _& [1 ~( O3 w9 O) y4 p6 q6 R
第1步,分解问题
! Q/ ?2 D- A. I9 J1)要求解的问题:取出的巧克力,来自1号碗的概率是多少?
; D8 D' B+ [9 ^# [来自1号碗记为事件A1,来自2号碗记为事件A2
3 c% g, R3 H) m# j7 j8 L8 T取出的是巧克力,记为事件B,* }+ P0 J, \, C. R* Z
那么要求的问题就是P(A1|B),也就是取出的是巧克力(B),来自1号碗(A1)的概率
1 k3 ]4 i: d: m! A/ K/ A2)已知信息:" L$ t. N! t+ X+ B7 g& S
1号碗里有30个巧克力和10个水果糖5 n7 q+ S% F1 e/ j3 O
2号碗里有20个巧克力和20个水果糖8 J5 B& w# t% Q9 s7 g/ R
取出的是巧克力3 r% U/ F1 y; \+ i
/ w1 a3 I# K2 j0 \第2步,应用贝叶斯定理9 [2 h( j+ z- B/ y* Y: H. i2 i" b
3 I: K" @, F. ?9 c# k/ Y; D9 [+ S$ f! x
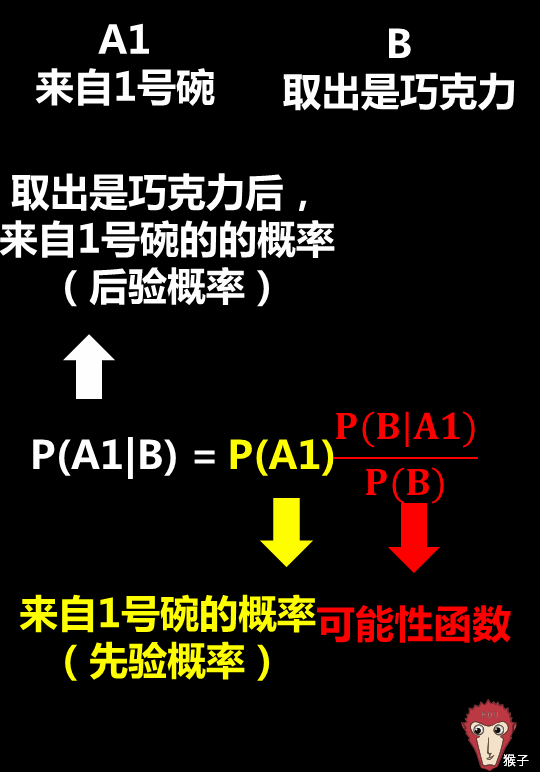
: Y ]- p Y" L" k' d- o( d/ t1)求先验概率% J9 ^! w1 @. {! {" I
由于两个碗是一样的,所以在得到新信息(取出是巧克力之前),这两个碗被选中的概率相同,因此P(A1)=P(A2)=0.5,(其中A1表示来自1号碗,A2表示来自2号碗)
' l/ p- H7 O! I9 g这个概率就是&#34;先验概率&#34;,即没有做实验之前,来自一号碗、二号碗的概率都是0.5。
8 |! R! P! ^7 j" Y/ m& k) h9 y# _
/ i6 |1 b7 X" t4 q& g. }9 {0 x: w8 H2)求可能性函数* r( I3 d8 l8 [' ?: A9 B: r6 N& y( q
P(B|A1)/P(B)$ \- L+ O7 G- [( `8 E6 y
其中,P(B|A1)表示从1号碗中(A1)取出是巧克力(B)的概率。1 U& w) c6 z) y# [& m
因为1号碗里有30个巧克力和10个水果糖,所以P(B|A1)=巧克力数(30)/(糖果总数30+10)=75%: j8 [$ D8 D3 U
现在贝叶斯公式里只剩P(B)了,只有求出P(B)就可以得到答案。- {$ v( H0 ~7 @
根据全概率公式,可以用下图求得P(B):
4 N4 y, V: k, k# H, G
9 Y' g; E& t X( U+ ?, Z( ^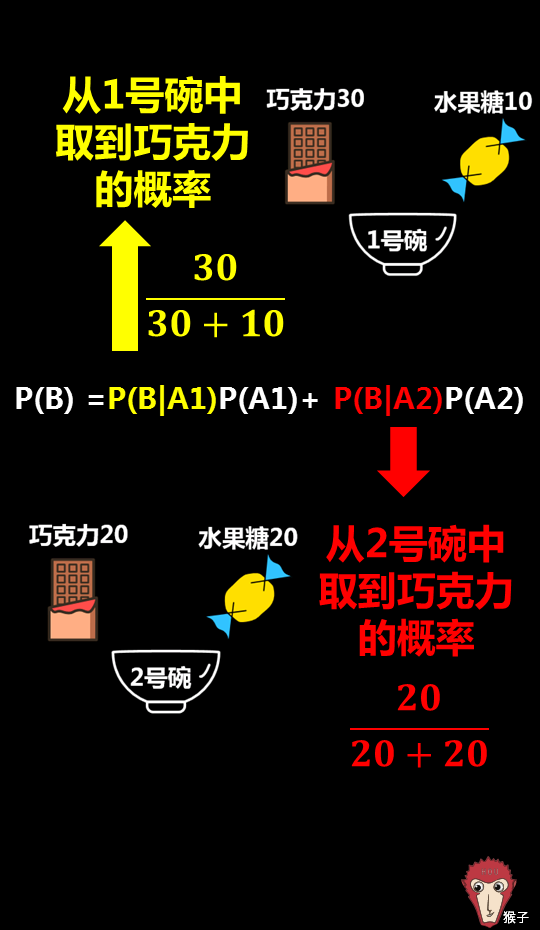
8 G& _" N9 o0 ?: y! h& X" Z: X$ Q图中P(B|A1)是1号碗中巧克力的概率,我们根据前面的已知条件,很容易求出。+ |9 g& R1 ~$ ^8 i& [- K
同样的,P(B|A2)是2号碗中巧克力的概率,也很容易求出(图中已给出)。
; R* a- O' K$ x* B ^$ Y而P(A1)=P(A2)=0.5' Q# [5 Q& u) z- D U; `
将这些数值带入公式中就是小学生也可以算出来的事情了。最后P(B)=62.5%/ Z Q7 L' `! |7 K8 \8 `' u
9 W. q5 E+ L. o2 I, M* N所以,可能性函数P(B|A1)/P(B)=75%/62.5%=1.2。
5 f8 K8 V7 ^" F! x) X1 r可能性函数>1.表示新信息B对事情A1的可能性增强了。
( ?; p" g; ~3 V h' @: |0 `$ K
; v8 q! T7 i8 L, ~7 L/ A3)带入贝叶斯公式求后验概率
% A) Y" P% |" X1 r# T- T0 e将上述计算结果,带入贝叶斯定理,即可算出P(A1|B)=60%! \2 Q) P; v; E' a! ]7 C( N+ O) m. X
$ b! c9 [4 Y0 f- A0 W: h# h$ c
 ; ~8 Z; L6 R) J. w' P ; ~8 Z; L6 R) J. w' P
这个例子中我们需要关注的是约束条件:抓出的是巧克力。如果没有这个约束条件在,来自一号碗这件事的概率就是50%了,因为巧克力的分布不均把概率从50%提升到60%。( v" q8 H: L. J( @2 G: q* l
' r2 ?8 Y1 y/ r: u9 j) I
现在,我总结下刚才的贝叶斯定理应用的套路,你就更清楚了,会发现像小学生做应用题一样简单:: ]. w; E9 ^# B' r2 `+ ~
第1步. 分解问题
+ U. E# B: A1 R$ ?7 e5 Y; L: K9 v简单来说就像做应用题的感觉,先列出解决这个问题所需要的一些条件,然后记清楚哪些是已知的,哪些是未知的。& K$ Y% j4 D( b
1)要求解的问题是什么?4 a v$ o, l% K3 u" C( k8 g2 n
识别出哪个是贝叶斯中的事件A(一般是想要知道的问题),哪个是事件B(一般是新的信息,或者实验结果)
. K1 @0 @7 X! P2)已知条件是什么?
% e1 u5 p, x; v5 m" [, C% }+ g6 n2 n- z0 \) n2 ~" J, O: u
第2步.应用贝叶斯定理
4 q( k1 n4 ]- O9 Z" r7 O' b第3步,求贝叶斯公式中的2个指标& s/ e. p. n' y, O
1)求先验概率$ e( V# p* {9 [ b& i) e# P) _
2)求可能性函数& W$ r/ V2 U( \# f
3)带入贝叶斯公式求后验概率
3 p. ~0 e1 u9 C: B t1 V
* K0 u$ a, H' \' M" S' S+ c4 n6 z
3 [( r/ U4 k, C
" Y0 C: A. Q! W案例2:贝叶斯定理在医疗行业的应用
. m* X% j% }( Z [% |每一个医学检测,都存在假阳性率和假阴性率。假阳性,就是没病,但是检测结果显示有病。假阴性正好相反,有病但是检测结果正常。
/ S" v! Y' Q) e& o& a即使检测准确率是99%,如果医生完全依赖检测结果,也会误诊。也就是说假阳性的情况,根据检测结果显示有病,但是你实际并没有得病。5 Z$ j- W9 `6 D+ ?
举个更具体的例子,因为艾滋病潜伏期很长,所以即便感染了也可能在很长的一段时间,身体没有任何感觉,所以艾滋病检测的假阳性会导致被测人非常大的心理压力。2 }0 A% e" t0 z& b: ^8 [
+ A( m& L% [4 e# a# x [, d4 b
你可能会觉得,检测准确率都99%了,误测几乎可以忽略不计了吧?所以你觉得这人肯定没有患艾滋病了对不对?/ @8 Q+ a" B/ z9 [
让我们用贝叶斯定理算一下,就会发现你的直觉是错误的。
& l: q# o( M( W- \ r2 n1 H2 x6 O# N
假设某种疾病的发病率是0.001,即1000人中会有1个人得病。现在有一种试剂可以检验患者是否得病,它的准确率是0.99,即在患者确实得病的情况下,它有99%的可能呈现阳性。它的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性。
( t: c( U( O+ ?/ T$ J3 q" G0 I1 {" V I现在有一个病人的检验结果为阳性,请问他确实得病的可能性有多大?
1 Y: r+ M( v# E
9 b4 `, V( ^7 c& i& O% K4 g好了,我知道你面对这一大推信息又头大了,我也是。但是我们不是有贝叶斯模板套路嘛,下面开始。* c0 X. j7 `3 r4 ?1 N" H0 ?9 }
6 q& e) ?4 b; {/ X! c第1步,分解问题
5 p2 y1 j& x5 |+ K ?8 u+ L1)要求解的问题:病人的检验结果为阳性,他确实得病的概率有多大?
; e. ?6 P' R) [0 d, L" ?0 R( s病人的检验结果为阳性(新的信息)记为事件B,他得病记为事件A,
9 n9 ?1 b1 p, j+ p: {那么要求的问题就是P(A|B),也就是病人的检验结果为阳性(B),他确实得病的概率(A)
% N+ V" J# k0 _. l3 v7 Q3 e2)已知信息. e u8 ~7 C* p" c1 E
这种疾病的发病率是0.001,即P(A)=0.001) U6 v, l4 V0 [* @9 P
试剂可以检验患者是否得病,准确率是0.99,也就是在患者确实得病的情况下(A),它有99%的可能呈现阳性(B),所以P(B|A)=0.99
% J7 V f+ Q( }* K* }6 O: n试剂的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性。得病我们记为事件A,那么没有得病就是事件A的反面,记为A&#39;,所以这句话就可以表示为P(B|A&#39;)=5%
) ]6 f6 s7 x$ ?7 R# c1 ]5 ^3 X/ c& N4 k' E
2.应用贝叶斯定理
9 _' l- j' [7 g, r. ^ w- Q T- I( d; h; \! G& J
 . x/ ?0 Z* M1 U' ]) F i . x/ ?0 Z* M1 U' ]) F i
1)求先验概率% g, G- T+ C0 P7 n1 v
疾病的发病率是0.001,即P(A)=0.0010 f8 ?) \7 E+ {/ M& @5 d/ Z
2)求可能性函数- D, W* _* w& K/ u3 h; u4 T7 Y
P(B|A)/P(B)
, _4 v/ V0 a. ?* s其中,P(B|A)表示在患者确实得病的情况下(A),试剂呈现阳性的概率,从前面的已知条件中我们已经知道P(B|A)=0.99
: t) D; w5 X" i* G! R) o n现在只有求出P(B)就可以得到答案。根据全概率公式,可以用下图求得P(B)=0.05094! u1 p' W" F0 E5 m" d
, Q( c) U, u( E1 x( o& p0 y * }# X, l/ D f4 m* Q; b3 H * }# X, l/ D f4 m* Q; b3 H
所以可能性函数P(B|A)/P(B)=0.99/0.05094=19.4346* m/ |0 A( S' |
3)带入贝叶斯公式求后验概率- q6 A7 W/ T/ G& T. a# z; y% W
我们得到了一个惊人的结果,P(A|B)等于1.94%。6 e1 U( O6 ?1 j- L
也就是说,筛查的准确率都到了99%了,通过体检结果有病(阳性)确实得病的概率也只有1.94%1 `2 F( ^/ ^5 {1 H5 ^- L4 ~" D% }
- e f0 l2 ?3 f [( P5 ?' Q; Z% P

. V2 J& x( |( `( A6 Q- m1 t你可能会说,再也不相信那些吹的天花乱坠的技术了,说好了筛查准确率那么高,结果筛查的结果对于确诊疾病一点用都没有,这还要医学技术干什么?
0 z& p! E& |) c没错,这就是贝叶斯分析告诉我们的。我们拿艾滋病来说,由于发艾滋病实在是小概率事件,所以当我们对一大群人做艾滋病筛查时,虽说准确率有99%,但仍然会有相当一部分人因为误测而被诊断为艾滋病,这一部分人在人群中的数目甚至比真正艾滋病患者的数目还要高。
! p: |5 r$ W h7 z2 v# }/ i
3 x! F8 B; z7 i- y3 I你肯定要问了,那该怎样纠正测量带来这么高的误诊呢?
( T# L. ~0 ^( Q9 b# X) A造成这么不靠谱的误诊的原因,是无差别地给一大群人做筛查,而不论测量准确率有多高,因为正常人的数目远大于实际的患者,所以误测造成的干扰就非常大了。
. c) u1 J/ [& G% |! n7 [' n' y' z8 {& Q0 X ]" c m
根据贝叶斯定理,我们知道提高先验概率,可以有效的提高后验概率。4 i; E: ~( D1 l, r
所以解决的办法倒也很简单,就是先锁定可疑的人群,比如10000人中检查出现问题的那10个人,再独立重复检测一次。因为正常人连续两次体检都出现误测的概率极低,这时筛选出真正患者的准确率就很高了,这也是为什么许多疾病的检测,往往还要送交独立机构多次检查的原因。
9 j- |8 G! `8 @3 _0 @, t t! D这也是为什么艾滋病检测第一次呈阳性的人,还需要做第二次检测,第二次依然是阳性的还需要送交国家实验室做第三次检测。2 q) i% o7 |/ X
在《医学的真相》这本书里举了个例子,假设检测艾滋病毒,对于每一个呈阳性的检测结果,只有50%的概率能证明这位患者确实感染了病毒。但是如果医生具备先验知识,先筛选出一些高风险的病人,然后再让这些病人进行艾滋病检查,检查的准确率就能提升到95%。4 x2 R: w$ \% n5 V( k" s# E
! _3 F& N+ O7 v# p0 z% w案例4:贝叶斯垃圾邮件过滤器/ G8 P: ~" H- |% @3 v
垃圾邮件是一种令人头痛的问题,困扰着所有的互联网用户。全球垃圾邮件的高峰出现在2006年,那时候所有邮件中90%都是垃圾,2015年6月份全球垃圾邮件的比例数字首次降低到50%以下。& h3 w$ A9 a, x
最初的垃圾邮件过滤是靠静态关键词加一些判断条件来过滤,效果不好,漏网之鱼多,冤枉的也不少。
9 h7 W# ~) E9 S3 X! n% n9 H2002年,Paul Graham提出使用&#34;贝叶斯推断&#34;过滤垃圾邮件。他说,这样做的效果,好得不可思议。1000封垃圾邮件可以过滤掉995封,且没有一个误判。9 I) r9 H% C8 F. n. w( O
* n8 l1 X7 s4 @
因为典型的垃圾邮件词汇在垃圾邮件中会以更高的频率出现,所以在做贝叶斯公式计算时,肯定会被识别出来。之后用最高频的15个垃圾词汇做联合概率计算,联合概率的结果超过90%将说明它是垃圾邮件。
9 y/ R0 y( V* u8 ?. z, r# F
3 A4 `( w# L0 S* O& M& C; v3 n用贝叶斯过滤器可以识别很多改写过的垃圾邮件,而且错判率非常低。甚至不要求对初始值有多么精确,精度会在随后计算中逐渐逼近真实情况。" I3 G1 s- o& X+ b
(ps:如果留言想详细了解这个知识的很多,我后面会专门写文章来回答大家)8 W. Z0 g# g' s- K
" C7 c. m+ r8 \8 l4 [0 \
4.生活中的贝叶斯思维 贝叶斯定理与人脑的工作机制很像,这也是为什么它能成为机器学习的基础。6 O; t" Y6 h; q4 ^2 ]
如果你仔细观察小孩学习新东西的这个能力,会发现,很多东西根本就是看一遍就会。比如我3岁的外甥,看了我做俯卧撑的动作,也做了一次这个动作,虽然动作不标准,但也是有模有样。* c/ @6 T( o8 F B j! x" u
同样的,我告诉他一个新单词,他一开始并不知道这个词是什么意思,但是他可以根据当时的情景,先来个猜测(先验概率/主观判断)。一有机会,他就会在不同的场合说出这个词,然后观察你的反应。如果我告诉他用对了,他就会进一步记住这个词的意思,如果我告诉他用错了,他就会进行相应调整。(可能性函数/调整因子)。经过这样反复的猜测、试探、调整主观判断,就是贝叶斯定理思维的过程。- q6 G& W- }% e# T/ l5 b1 ?+ k
+ ^* R( x8 G" s r. V
同样的,我们成人也在用贝叶斯思维来做出决策。比如,你和女神在聊天的时候,如果对方说出“虽然”两个字,你大概就会猜测,对方后面九成的可能性会说出“但是”。我们的大脑看起来就好像是天生在用贝叶斯定理,即根据生活的经历有了主观判断(先验概率),然后根据搜集新的信息来修正(可能性函),最后做出高概率的预测(后验概率)。- \: E; z0 B: M4 e/ z; k
7 [5 C: L& A' U# k其实这个过程,就是下图的大脑决策过程:4 t& x7 d: n" ]6 l
% q( s( {$ h3 t& k! }3 s
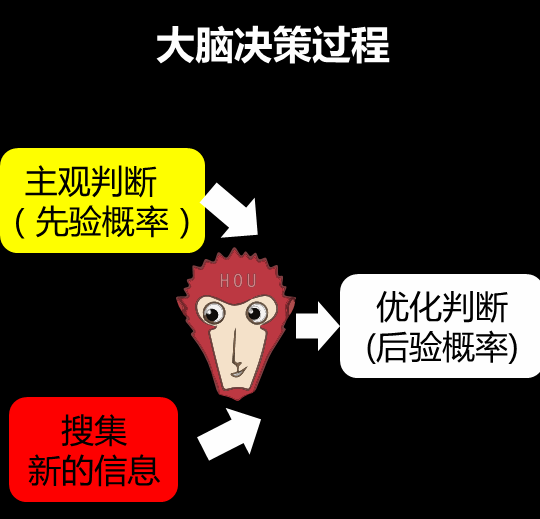
; B. w8 v2 W) Q0 | H" X f) B+ y/ `8 J- @: `所以,在生活中涉及到预测的事情,用贝叶斯的思维可以提高预测的概率。你可以分3个步骤来预测:
) A; p3 C: e# u2 H. n! p9 S1 Y1 R1.分解问题2 p. w0 h& [) R# z3 w. b7 ]! n- d
简单来说就像小学生做应用题的感觉,先列出要解决的问题是什么?已知条件有哪些?2 h* P' W4 w( Q6 l$ A/ H" s
2. 给出主观判断# b1 t. r8 L; Z7 E
不是瞎猜,而是根据自己的经历和学识来给出一个主观判断。
; _; H N" O* e4 G3.搜集新的信息,优化主观判断. e3 m" o/ ^0 c7 V n8 g' _7 i2 V
持续关于你要解决问题相关信息的最新动态,然后用获取到的新信息来不断调整第2步的主观判断。如果新信息符合这个主观判断,你就提高主观判断的可信度,如果不符合,你就降低主观判断的可信度。1 e) {! T/ F$ V! ^ ~/ p5 m
+ C5 T E! e6 S# q$ o" R# @* Y: a
比如我们刚开始看到“人工智能是否造成人类失业”这个信息,你有自己的理解(主观判断),但是当你学习了一些数据分析,或者看了些这方面的最新研究进展(新的信息),然后你根据掌握的最新信息优化了自己之前的理解(调整因子),最后重新理解了“人工智能”这个信息(后验概率)。这也就是胡适说的“大胆假设,小心求证”。) a. x& Z% _' K# c: Y7 w
+ `+ v& p* @8 X- G( X% G
概率的基础知识补充:
+ t' W$ L! z3 h1 a- E+ L% C7 G. @5 W- z9 t7 M5 k) N
参考资料:
- ^& t) Y6 @& k! t$ HYouTube英文视频《Thomas Bayes: Probability for Success》
! `$ i: Y+ V* D$ s1 i& z- nYouTube英文视频《Everything You Ever Wanted to Know About Bayes&#39; Theorem But Were Afraid To Ask.》8 H8 _8 e# M; H+ I3 D
贝叶斯垃圾邮件过滤器:http://www.paulgraham.com/spam.html
- z9 [/ L, S/ L$ w贝叶斯垃圾邮件过滤Wiki:https://en.wikipedia.org/wiki/Naive_Bayes_spam_filtering4 q5 Q% ~+ [1 d4 s" Z
贝叶斯推断及其互联网应用(一)& N; D$ t! S$ C$ I8 L5 N* i. i
《联邦党人文集》背后的统计学幽灵 |